They are implementations of the class KernelOnPairs and operate on instances of the class ExamplePair.
Preference Kernel
Java class: PreferenceKernel
Source code: PreferenceKernel.java
Maven Project: kelp-core
JSON type: preference
Description: in the learning to rank scenario, the preference kernel (Shen and Joshi, 2003) compares two pairs of ordered objects ![]() and
and ![]() :
:
![]()
where BK is a generic kernel operating on the elements of the pairs. The underlying idea is to evaluate whether the first pair![]() aligns better to the second pair in its regular order
aligns better to the second pair in its regular order![]() rather than to its inverted order
rather than to its inverted order![]() .
.
Parameters:
- baseKernel: the base kernel BK applied over the elements of the pairs.
Uncrossed Pairwise Sum Kernel
Java class: UncrossedPairwiseSumKernel
Source code: UncrossedPairwiseSumKernel.java
Maven Project: kelp-core
JSON type: uncrossedPairwiseSum
Description: it compares two pairs of ordered objects ![]() and
and ![]() , summing the contributions of the single element similarities:
, summing the contributions of the single element similarities:
![]()
where BK is a generic kernel operating on the elements of the pairs. It has been used in learning scenarios where the elements within a pair have different roles, such as text and hypothesis in Recognizing Textual Entailment (Filice et al., 2015), or question and answer in Question Answering (Filice et al., 2016).
Parameters:
- baseKernel: the base kernel BK applied over the elements of the pairs.
- intrapairSimProduct: whether adding or not to the kernel combination an extra term equivalent to the multiplication of the intra-pair similarities, i.e.,
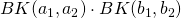 .
.
Uncrossed Pairwise Product Kernel
Java class: UncrossedPairwiseProductKernel
Source code: UncrossedPairwiseProductKernel.java
Maven Project: kelp-core
JSON type: uncrossedPairwiseProduct
Description: it compares two pairs of ordered objects ![]() and
and ![]() , multiplying the contributions of the single element similarities:
, multiplying the contributions of the single element similarities:
![]()
where BK is a generic kernel operating on the elements of the pairs. As for the UncrossedPairwiseSumKernel, it has been used in learning scenarios where the elements within a pair have different roles, such as text and hypothesis in Recognizing Textual Entailment (Filice et al., 2015), or question and answer in Question Answering (Filice et al., 2016). The product operation inherently applies a sort of logic and between the ![]() and
and ![]() .
.
Parameters:
- baseKernel: the base kernel BK applied over the elements of the pairs.
- intrapairSimProduct: whether adding or not to the kernel combination an extra term equivalent to the multiplication of the intra-pair similarities, i.e.,
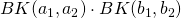 .
.
Pairwise Sum Kernel
Java class: PairwiseSumKernel
Source code: PairwiseSumKernel.java
Maven Project: kelp-core
JSON type: pairwiseSum
Description: it compares two pairs of objects ![]() and
and ![]() , summing the contributions of all pairwise similarities between the single elements:
, summing the contributions of all pairwise similarities between the single elements:
![]()
where BK is a generic kernel operating on the elements of the pairs. It has been used in symmetric tasks, such as Paraphrase Identification, where the elements within a pair are interchangeable (Filice et al., 2015).
Parameters:
- baseKernel: the base kernel BK applied over the elements of the pairs.
- intrapairSimProduct: whether adding or not to the kernel combination an extra term equivalent to the multiplication of the intra-pair similarities, i.e.,
 .
.
Pairwise Product Kernel
Java class: PairwiseProduct
Source code: PairwiseProduct.java
Maven Project: kelp-core
JSON type: pairwiseProduct
Description: it compares two pairs of objects ![]() and
and ![]() , summing the contributions of the two possible pairwise alignments:
, summing the contributions of the two possible pairwise alignments:
![]()
where BK is a generic kernel operating on the elements of the pairs. It has been used in symmetric tasks, such as Paraphrase Identification, where the elements within a pair are interchangeable (Filice et al., 2015).
Parameters:
- baseKernel: the base kernel BK applied over the elements of the pairs.
- intrapairSimProduct: whether adding or not to the kernel combination an extra term equivalent to the multiplication of the intra-pair similarities, i.e.,
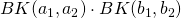 .
.
Best Pairwise Alignment Kernel
Java class: BestPairwiseAlignmentKernel
Source code: BestPairwiseAlignmentKernel.java
Maven Project: kelp-core
JSON type: bestPairwiseAlignment
Description: it compares two pairs of objects![]() and
and ![]() , evaluating the best pairwise alignment:
, evaluating the best pairwise alignment:
![]()
where BK is a generic kernel operating on the elements of the pairs, and softmax is a function put in place of the max operation, which would cause K not to be a valid kernel function (i.e., the resulting Gram matrix can violate the Mercer’s conditions). In particular,![]() (c=100 is accurate enough). The BestPairwiseAlignmentKernel has been used in symmetric tasks, such as Paraphrase Identification (Filice et al., 2015), where the elements within a pair are interchangeable.
(c=100 is accurate enough). The BestPairwiseAlignmentKernel has been used in symmetric tasks, such as Paraphrase Identification (Filice et al., 2015), where the elements within a pair are interchangeable.
Parameters:
- baseKernel: the base kernel BK applied over the elements of the pairs.
- intrapairSimProduct: whether adding or not to the kernel combination an extra term equivalent to the multiplication of the intra-pair similarities, i.e.,
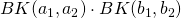 .
.
References
Simone Filice, Giovanni Da San Martino and Alessandro Moschitti. Relational Information for Learning from Structured Text Pairs. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics, ACL 2015.
Simone Filice, Danilo Croce, Alessandro Moschitti and Roberto Basili. KeLP at SemEval-2016 Task 3: Learning Semantic Relations between Questions and Answers. In Proceedings of the 10th International Workshop on Semantic Evaluation (SemEval 2016), Association for Computational Linguistics. (Best system @ SemEval-2016 task 3)
Libin Shen and Aravind K. Joshi. An svm based voting algorithm with application to parse reranking. In In Proc. of CoNLL 2003, pages 9–16, 2003